Abstract
The use of testing electrodes on the surface of the earth to simulate human feet, in assessing the electrical safety of grounding systems, requires particular care to avoid misleading results. The concern is the variability in the electrical characteristics of the probe in contact with the earth. The subject is analyzed in this paper and potential solutions are identified for the two major concerns: earth contact impedance and earth spreading resistance. A proposed methodology is outlined that makes it possible to perform one-time measurements of the maximum touch current at a particular site.
Introduction
Establishing safety criteria when electric current is expected to flow through the human body has been difficult; research on this subject has been going on for many decades. The problem is the many parameters with poorly defined and difficult to measure variabilities. The response of children to body current is an example; the response can only be theorized based on testing conducted on adults and animals, and using body mass as the scaling factor.
There are uncertainties in characterizing the human body and its response to electric current, but also in trying to characterize the earth and other situational factors. The International Electrotechnical Commission Report 479-1 [1] provides a summary of what has been learned on the subject of current passing through the human body, as well as a good bibliography of the research work on this matter. Standards such as ANSI/IEEE Std 80-186 [2], IEEE Std 81-1983 [3], and ANSI/IEEE Std 142-1982 [4] provide information and guidelines that deal with situational factors, primarily aimed at electrical power systems.
While the problem is basically one of determining the maximum current that is safe for human beings, it is dealt with mostly in terms of finding the maximum touch voltage. The restatement of the problem in terms of voltage is useful, because it transforms a problem which is intrinsically stochastic into a more deterministic one, since in most situations the source voltage is fixed or can be measured more easily. This restatement in terms of voltages becomes even more valuable at levels under 50 V, where the skin impedance of the human body is highly dependent on the touch voltage itself [1].
A stochastic problem is turned into a deterministic one for problem manageability, by assuming a worst-case scenario. This tends to be a haphazard endeavor with many subjective judgments, because many of the variables are not known very well in terms of their statistical variability. The results can be very conservative safety criteria, with no statistical characterization, that result in preventing problems which have only as much likelihood as the 100-year flood. However, with the ethical obligation and the legal requirement to ensure the safety of the system, the search continues to resolve the variability problem of many of these parameters.
In the assessment of a specific situation, standard assumptions have to be made about people, because the variables dealing with people and the human body are too wide-ranging and generic to be addressed in this context. However, other situational variables might be controllable; these include contact resistance and earth resistance. If it were possible to measure the worst-case current that can be expected at a specific place or setting, by controlling contact resistance and earth resistance, then the safety criterion could be based on maximum touch current rather than maximum touch voltage. In other words, rather than measure touch potential and evaluate safety by a voltage criterion that by implication assures a safe current, based on suppositions about contact resistance and earth resistance, measure the touch current directly by eliminating the contact resistance and including the actual earth in question in its most conductive state. In order to do this, the situational variables must be controlled, so that the measurement is credible. To be credible, the measurement protocol has to yield the same worst-case current value no matter how many times the measurement is repeated and no matter what the meteorological conditions are. What is needed is a protocol for measuring the maximum touch current in a given situation, given the standard assumptions about the human body conductivity to electric current.
Problem Description
An analysis of field test data was conducted in a previous paper [5] to determine the appropriate technique and instrumentation to measure step potentials and simulated body currents. It was concluded that while the use of flat disk probes laid on the surface of the earth was most representative of a person standing, it provided the most variability in measuring both voltage and current. In contrast, a short rod electrode (~8 in) of an equivalent resistance to earth, inserted vertically in the earth surface, provides less measurement variability. However, the rod is usable only in soft and loose material; it cannot be used on hard surfaces. Furthermore, it does not replicate correctly the situation of a person standing, which may lead to unrealistic and detrimental assessments in certain cases. It was also noted in that study that the variability is much higher for current than for voltage measurements. The conclusion reached in that paper [5] is that the combination of contact and spreading resistance between the electrode and earth is the source of most of the data variability.
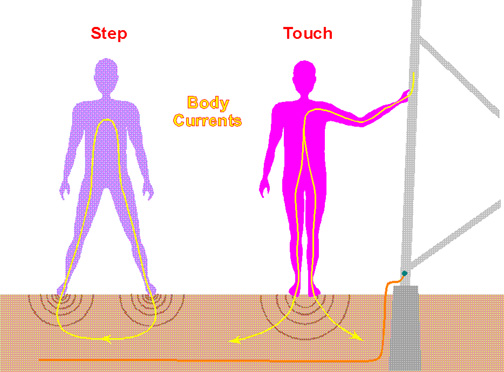
The measurements addressed in that paper were step voltage and simulated body currents. Figure 1 illustrates the body path for step and touch currents, which form the basis for both voltage and current measurements. Step and touch current measurements are similar because they both involve contact with earth. They differ in their path through the human body. The current enters the human body at one foot and leaves at the other foot in the step current or potential case; and the current enters the human body at one or both hands and leaves at both feet in a touch current or voltage situation. This paper will be confined to touch current and voltage, with the results capable of being extended to step current and voltage.

As shown in Figure 2, the circuit elements that limit the amount of current that flows through the human body can be defined to be: (1) the hand contact impedance, (2) the body total impedance, (3) the earth contact impedance, and (4) the earth spreading resistance. The hand contact impedance is taken to be zero, because the structure that is often of concern is metallic and has very little resistivity compared to the other elements in the circuit. In a measurement setting, one needs only to make sure that the electrical probe makes a good contact with the bare metal of a structure, avoiding rust spots and protective layers such as paint.
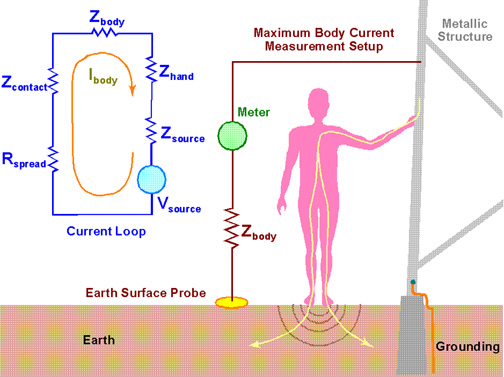
The skin contact impedance and spreading resistance into the human body are included in the body total impedance, which is based on the assumption that the hand surface contact area is of 50-100 cm2 [1]. The total body impedance varies with voltage as indicated in Ref. 1. The gradient of the impedance is high at low voltages, and then decreases as the voltage rises, until the impedance levels off above 150 V ac. A conservative figure for of the total body impedance below 50 V is 1,500 , for 5% of the population (the most sensitive people). Ref. 1 does not address voltages below 25 V but, using interpolation, a value for total body impedance for the conservative 5% of the population is estimated to be 2,000 at around 10 V. The body total impedance can be simulated in a measurement setting by a fixed resistor or a number of resistors that cover the range of interest (see Table I in Ref. 1).
Shoes and other footwear are normally worn by people and can provide considerable resistance to electric current flowing to earth through the human body. This is especially true with modern shoes that use synthetic material for soles, materials that can be very good electrical insulators. The convention in a worst-case scenario is to assume zero electrical resistance for shoes and other footwear. This assumption seems excessively conservative in view of the perception that most people ordinarily do wear shoes. In the author's experience, however, the assumption is tenable for two reasons, wetness and the kneeling scenario. In the presence of precipitation and in wet terrains, shoes and other footwear can get wet to the point of providing minimal resistance. Kneeling down on earth is a scenario similar to a step that is ignored, but is more dangerous. In a kneeling situation, the body skin is in direct contact with the earth or is insulated by a thin layer of clothing that can be rendered conductive by the moisture in the earth. The assumption of zero impedance for shoes and clothing in the path of currents traveling though the human body is, therefore, a reasonable worst-case assumption.

The earth contact impedance is the source of much concern, because the surface will vary greatly in nature and composition, and will also vary cyclically through the seasons [6]. It is conventional [2] to assume that the foot of a human can be simulated by using a flat metallic plate with a surface area of 201 cm2 (31.2 in2), typically a round disk with a radius of 8 cm (3.15 in). To simulate correctly the foot of a human being standing, the disk should be loaded with a weight, although this is not mentioned much in the literature. If the typical human being assumed in Ref. 2 weighs 50 kg (110 lbs), this translates into a weight of 25 kg (55 lbs) per foot, or disk probe.
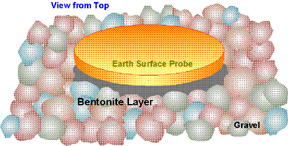
The size of the disk is actually not important in measuring voltages, because the contact resistance, if not excessive, will not affect the measurement done with an high-impedance meter. However, the contact resistance, which depends on the size of the disk probe, will affect the current measurement, because it is in the series loop that limits the body current (see Figure 2). The problem of contact resistance is illustrated in Figure 3, where a disk probe is laid on top of large gravel. In this extreme case, the disk makes contact with earth through three points, since it takes only three points to define a plane. Hard surfaces such as asphalt, concrete, or packed gravel, present similar problems. A different kind of problem is presented in soft terrain resulting from naturally occurring vegetation or other organic material. The use of a rod in place of a disk to limit the contact resistance is an unsatisfactory answer. The rod is useless in the case of hard surfaces, and creates its unique problems when forced into semi-hard terrain by causing tapered holes that result in poor contact. As mentioned earlier, the rod also tends to distort the picture in a detrimental fashion, especially in cases where the earth electrode that is the source of the voltage or current being measured is buried at shallow depths.
The spreading resistance into the earth under a foot is also a variable, although not as much a concern as the contact impedance. This resistance changes greatly over time in response to meteorological conditions [6]. This resistance is localized in the top layer of the earth, a layer that is exposed to the elements and is greatly affected by temperature and moisture conditions. The changes include both random and cyclical effects; the cycles are based on diurnal and seasonal patterns. Some surfaces are more sensitive to these variations than others. Bogs and wetlands tend to have more constant spreading resistance throughout the year. Sandy terrains, on the other hand, have a highly variable spreading resistance; it is very low during rainy periods, but as the sandy soil drains, the spreading resistance returns to the high value typical of dry conditions. Frost at northen latitudes is another source of extreme variability in spreading resistance; the resistance is very high during freeze periods and very low during thawing.
The variability encountered in practice with the contact impedance and spreading resistance using flat earth electrodes is so great that any current measurement can be considered a random number of no particular significance. Even voltage measurements can be affected seriously when using such electrodes. For the latter, it may be simpler and more accurate to use a screwdriver driven into the earth or a wet sponge resting on a hard surface.
Proposed Solutions
There are possible solutions for these problems. The goal is to reduce or eliminate entirely the variabilities associated with earth contact impedance and spreading resistance in order to make reliable maximum touch current measurements.
For the contact impedance, a proposed solution is to use a jelly-like conductive material to fill the voids left between the flat probe and the earth surface. A good candidate for this material is sodium bentonite. Bentonite is a natural clay of volcanic origin, noncorrosive, stable, and inexpensive. Because it is a naturally occurring material, it will not contaminate or present any ecological problem. Bentonite needs a lot of water to achieve its main characteristics; at 300% moisture content, it has a resistivity of 2.5 ·m. Bentonite, which is readily available in powder form, can be mixed with water to form a soft and sticky paste that can be applied as a thick layer to the bottom surface of the flat probe. The probe can then be applied to the earth surface and pressed firmly to form an ideal contact. Once applied properly and left undisturbed, the probe does not have to be loaded with any weight to achieve the simulation conditions, because an optimal contact has already been achieved between the probe and the earth.
A solution for the spreading resistance is to saturate the earth with water at the point of contact with earth. This is based on the fact that spreading resistance is concentrated next to the electrode. The most propitious conditions exist right after a rainfall, when the ground naturally becomes saturated with water. During wet seasons, the need of water for the saturation state may be met with a reasonable effort. The water saturation effort may become expensive during dry seasons or in dry climates. The amount of water needed to achieve saturation depends on the porousness of the earth and the amount of water already present. However, the volume of earth to be treated is the determining factor.
In a touch voltage situation, a person can be assumed to be standing with his feet close to each other or spread apart. The difference is the mutual coupling between the spreading resistances, one under each foot. Using the model in Ref. 2, the spreading resistance of two feet in parallel varies from 1.82 at 1-ft separation to 1.65 at 3-ft separation (where is the earth resistivity). Using the latter, it is calculated that a metallic disc with an equivalent spreading resistance of 1.65 must have a radius of 15.2 cm, or about 6 in (see identities below).
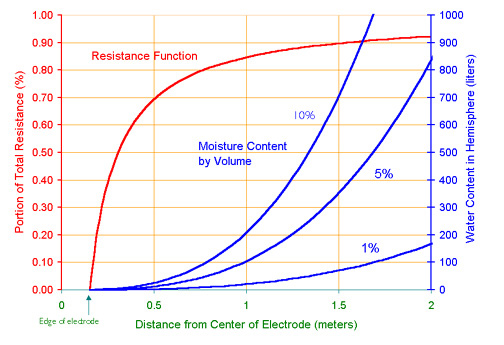
Figure 5 shows the spreading resistance gradient for the case of a hemispherical electrode, 15 cm in radius and flush with the surface of the earth, which closely describes the flat disk electrode. Most of the resistance is concentrated near the electrode: 75% of the resistance is within a radius of 0.61 m (2 ft) from the center of the electrode, and 90% within 1.52 m (5 ft). Figure 5 also shows the amount of water that is needed to bring the moisture content within the hemisphere defined by the radius described above to a given proportion by volume (1%, 5%, and 10%). The water requirements for the 5% moisture content are 24 liters (6.3 gallons) for the 75% portion of the total resistance, and 371 liters (98 gallons) for the 90% portion. Notwithstanding the dryness of the earth surface, there is always some moisture deeper below; therefore, the water requirements can be reduced substantially. The problem with water saturation can be substantial during dry seasons or in dry climates, especially with soils like sand that drain quickly. The question then is water availability and the cost to recreate a saturation state. Working during wet seasons and testing right after a substantial rainfall eases the water problem substantially.
The engineer has to work closely with geological and meteorological data to assess properly the water saturation needs. In the case of impermeable surfaces, such as those finished with bituminous material or concrete, it is still important to study the nature of the subsoil, and the seasonal variations to determine the need to recreate the most conductive conditions within the range of natural activity.
Measurement Protocol
A proposed measurement protocol for eliminating contact impedance and minimizing spreading resistance at the point of contact with earth using a disk electrode to assess the maximum touch current is as follows:
Conclusions
A testing methodology has been outlined that should help resolve the problem with contact impedance and spreading resistance when using flat, earth-surface electrodes to test for the maximum current that would flow through the body of a human being under simulated conditions. The proposed method affords a direct and accurate measurement of the simulated body current, resulting in less uncertainty and a better assessment of safety, compared to the alternative approach of using touch voltage measurements which are then used to deduce the body currents by making assumptions about contact impedance and spreading resistance.
The methodology is intended to improve and add to the measuring capability, by improving the reliability and significance of field measurements. By improving the quality of field data, it may be possible to make safety assessments that are more accurate and less costly in the long run. The use of bentonite is a simple procedure and will eliminate the contact resistance, which contributes significantly to the variability problem. The spreading resistance is a smaller problem in comparison but more complicated to resolve. The solution hinges on the accuracy desired and the water needs to simulate saturation, if the surface is porous. It makes the job easier to schedule such tests during wet seasons.
References