Pagina 4

        Descrizione del Modello Matematico

Il spreadsheet (foglio di calcolo) del modello matematico è illustrato nella pagina 3. È una successione di definizioni di variabili matematiche su seguenti righe di un foglio di calcolo, seguendo una testata (le prime dieci righe). La testata include informazioni di riferimento su questo foglio di calcolo (colonna A) e costanti precalcolate (colonne E-G). Le costanti precalcolate sono i valori trigonometrici per gli angoli nel triangolo caratteristico dell'ottagono.

Le informazioni su ciascuna riga sono disposte per colonne; i titoli per le colonne sono sulle righe 11-12. I dati includono una descrizione delle variabili (colonna B), il nome della variabile (colonna C), la formula per la definizione della variabile (colonna D) ed il calcolo effettivo della variabile, entrambi in piedi (colonna E ) e metri (colonna F). L'unità di misura è impostata nella cella F11 ed è una variabile in questo modello matematico; una discussione sull'unità di misura segue a pagina 7.

Le righe per le definizioni sono raggruppate in due sezioni principali, una in alto che si occupa del disegno concettuale (riga 14) e una seconda più in basso (riga 72) che riguarda la modifica alle torri. Ogni sezione è suddivisa in gruppi logici più piccoli sotto un'intestazione descrittiva. Il foglio di calcolo termina con la definizione di un numero di variabili corollarie.

La definizione delle variabili include occasionalmente una seconda definizione matematica, un controllo sulla definizione precedente (per esempio righe 33 e 38), nonché note e righe di verifica (per esempio righe 66 e 78). Questa implementazione del modello matematico include 129 righe.

Simboli sono assegnati alle variabili matematiche, ad esempio: t per la diagonale maggiore dell'ottagono, u per la diagonale minore ottagonale, s per il lato dell'ottagono, ecc. Le lettere maiuscole sono usate per l'ottagono di base e le lettere minuscole sono usate per l'ottagono della torre (per esempio, S per il lato dell'ottagono di base e s per il lato dell'ottagono della torre). I nomi delle variabili per l'ottagono della zoccolatura sono la stessa lettera dell'alfabeto raddoppiata; se s è il lato dell'ottagono della torre, ss è il lato dell'ottagono della zoccolatura.

L'algoritmo geometrico per la progettazione del disegno concettuale e l'algoritmo geometrico per la modifica alle torri forniscono il contesto e la spiegazione dettagliata per ciascuna di queste variabili, nonché le definizioni matematiche. Le Fig. 4, 5 e 6 danno una definizione grafica delle variabili.

Fig. 4. Riferimenti grafici per le variabili matematiche – planimetria.

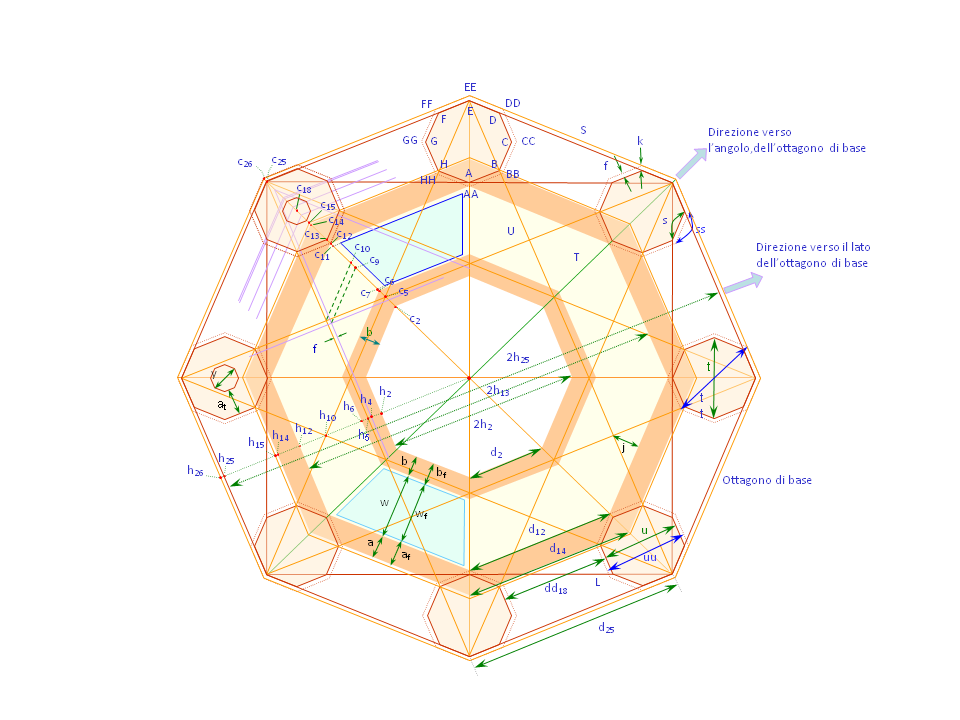
Fig. 5. Riferimenti grafici per le variabili matematiche – sezione dettagliata di un'ala del castello.

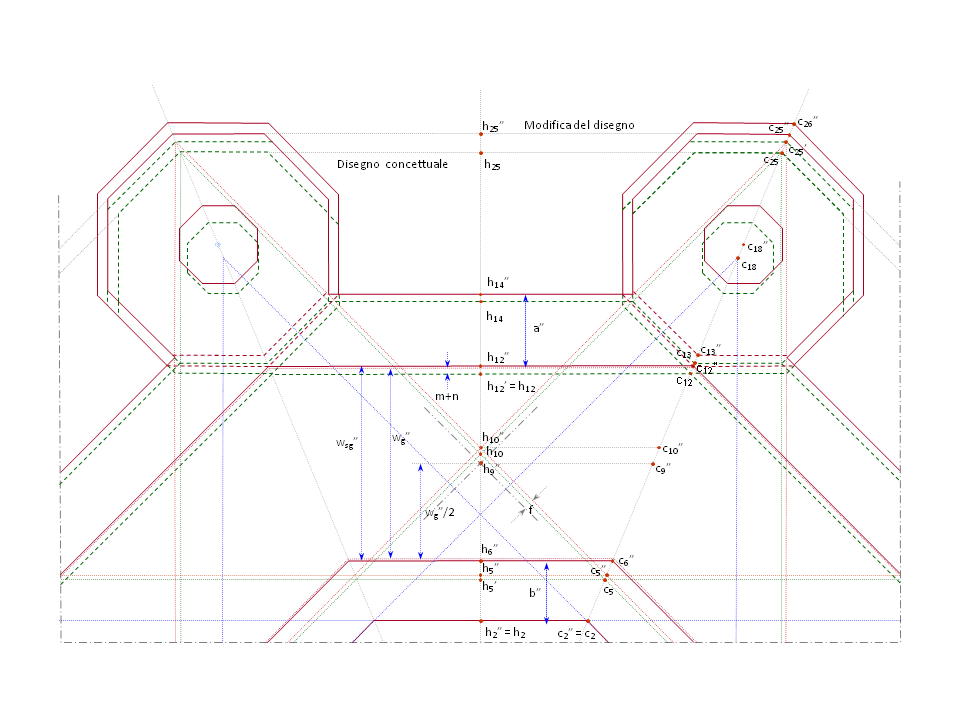
Fig. 6. Riferimenti grafici per le variabili matematiche – sezione dettagliata della torre.

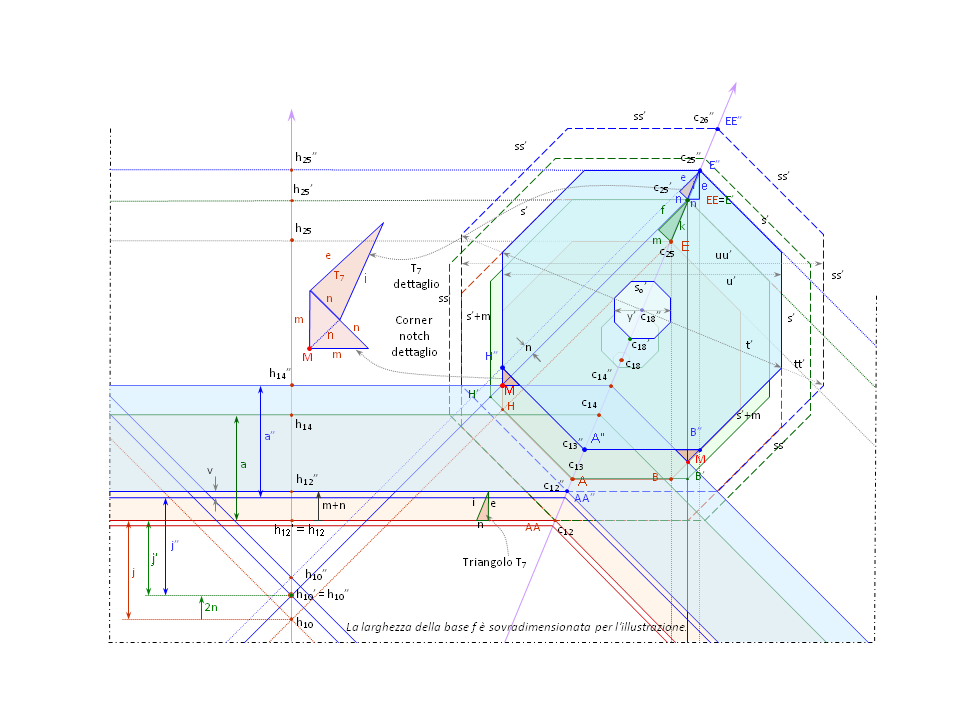
Tre variabili sono indicizzate numericamente; esse misurano la stessa caratteristica a diverse distanze dal centro nell'ottagono della pianta:

1. La variabile c misura la distanza dal centro dell'ottagono della pianta lungo la direzione dell'angolo dell'ottagono
2. La variabile h misura una distanza simile lungo la direzione dell'ala dell'ottagono della pianta (lato)
3. La variabile d misura il lato ottagonale a diverse distanze dal centro dell'ottagono della pianta

Per esempio: l'angolo dell'ottagono del cortile è c₂; l'angolo esterno dell'ottagono della torre, indicato altrove come angolo della torre E, è c₂₅ in questo modello matematico. Allo stesso modo d₂ è il lato dell'ottagono al perimetro del cortile, e d₂₅ è il lato dell'ottagono di base, indicato anche come S.

La distinzione tra le stesse variabili che cambiano posizione o dimensione passando dal disegno concettuale al disegno dela modifica delle torri è fatta con l'apice: nessun'apice nel disegno concettuale, apice semplice (') per il l'allargamento della torre e doppia (") per il riposizionamento della torre.

La progressione dell'apice della variabile viene congelata allo stato in cui la sua definizione non cambia più negli algoritmi. Per esempio, il lato della torre s cambia con l'ingrandimento dell'ottagono della torre, assumendo la dimensione s'. Tuttavia, non cambia più con il riposizionamento della torre; rimane alla definizione s' alla fine del modello matematico.

Le variabili indicizzate, c, d e h, sono anch'esse soggette a cambiamenti nella progettazione della modifica alle torri e sono di conseguenza etichettati con la notazione di apice semplice o doppia.

Ci sono alcune variabili incidentali con nomi unici o con pedici, con una spiegazione nella colonna delle descrizioni.

La colonna di definizione matematica fornisce la formula matematica. La maggior parte di queste formule sono elaborate nelle presentazioni dei modelli geometrici. Il resto si basano su relazioni geometriche.

Il modello matematico definisce le dimensioni delle forme in termini di unità, colonna E del spradsheet a pagina 3.

La variabile indipendente L, che è la dimensione laterale del quadrato di base, è assegnata una dimensione di 128 unità alla testa del modello, riga 15, colonna E. Una spiegazione per quest'assegnazione segue a pagina 5. Tutte le altre variabili sono calcolate in modo derivativo da questa misura.

Gli studiosi hanno preso in considerazione varie unità di misura storiche: il palmo, il cubito, il piede romano, ecc. All'unità di misura è assegnato un valore metrico nella cella F11, il foglio elettronico a pagina 3.

La colonna E fornisce il calcolo della dimensione per la variabile, nella unità di Castel del Monte. Queste misure vengono ricalcolate nella colonna F, a pagina 3 del spreadsheet, per l'equivalente valore metrico, utilizzando il valore metrico assegnato alla dimensione dell'unità di misura nella cella F11.

Tutte le dimensioni sono calcolate in metri (colonna F), in quanto le dimensioni sono riportate in metri.