Pagina 5

        Misticismo Medievale e l'Unità di Misura

La chiave per comprendere la progettazione architettonica è l'unità di misura. Non ci sono informazioni sui costruttori e sui lavori di costruzione di questo castello sin dal Medioevo. Non si sa nulla sull'unità di misura utilizzata nella progettazione e costruzione del castello, né sembra esserci evidenza di questa misura in nessuna parte del castello.

Gli studiosi hanno speculato sul cubito e sul palmo (Cardini 2000, 57), misure comuni da tempi antichi. H. Götze teorizza che l'unità di misura potrebbe essere stata il piede romano, approssimato a circa 0,3 m (Götze 1998, 169), che sembra riconciliarsi con le misure di alcune forme principali nella sua ipotesi del disegno della planimetria.

Il modello matematico è lo strumento utilizzato per scoprire l'unità di misura utilizzata nella progettazione e costruzione di Castel del Monte.

Tutte le forme della pianta sono derivate da una singola figura geometrica nell'algoritmo di progettazione, il quadrato di base. Questo è anche il caso nel modello matematico; le dimensioni di tutte le forme planimetriche sono ricavate nel foglio di calcolo in seguito all'assegnazione di una misura alla dimensione del quadrato di base L.

La dimensione del quadrato di base e l'unità di misura sono le uniche variabili indipendenti (incognite) in questo modello matematico. Conoscere una consente la determinazione dell'altra.

L'obiettivo dello studio è quindi quello di trovare la combinazione numerica di queste due variabili che dia la corrispondenza tra le dimensioni nella planimetria come calcolate nel modello matematico e le dimensioni effettive nella pianta.

Il spreadsheet è adetto nell'eseguire un'analisi iterativa per trovare la combinazione corretta di valori per L e la misura del piede come unità di misura. Tale analisi è ostacolata dalla mancanza di alcuni dati, dalla mancanza di precisione per alcune delle misure e da possibili errori o approssimazioni durante la costruzione 800 anni fa.

Tuttavia, la ricerca è facilitata da una serie di considerazioni. Il misticismo medievale fornisce indizi nella ricerca di una dimensione per la diagonale di base; questa è la diagonale comune fra l'ottagono di base ed il quadrato di base che vi è inscritto.

Le forme iniziali negli algoritmi di progettazione, il quadrato di base e l'ottagono di base, avevano un significato mistico nel Medioevo religioso. Attingiamo dalla cultura medievale e dalle note storiche per razionalizzare ciò che poteva essere concettualmente la misura primaria della diagonale di base.

È noto che nel simbolismo e nella religiosità della cultura medievale il quadrato era associato astrologicamente alla terra e religiosamente con uno stato di peccato e imperfezione. Il cerchio, d'altra parte, era associato con l'universo e l'infinito, e religiosamente ad uno stato di perfezione, Dio e il paradiso.

L'ottagono, che ha un quadrato inscritto dentro di se ed è a sua volta inscritto in un cerchio, è la figura di transizione tra il quadrato e il cerchio, Fig. 7.

Fig. 7. Ottagono, una forma geometrica di transizione tra il quadrato e il cerchio.

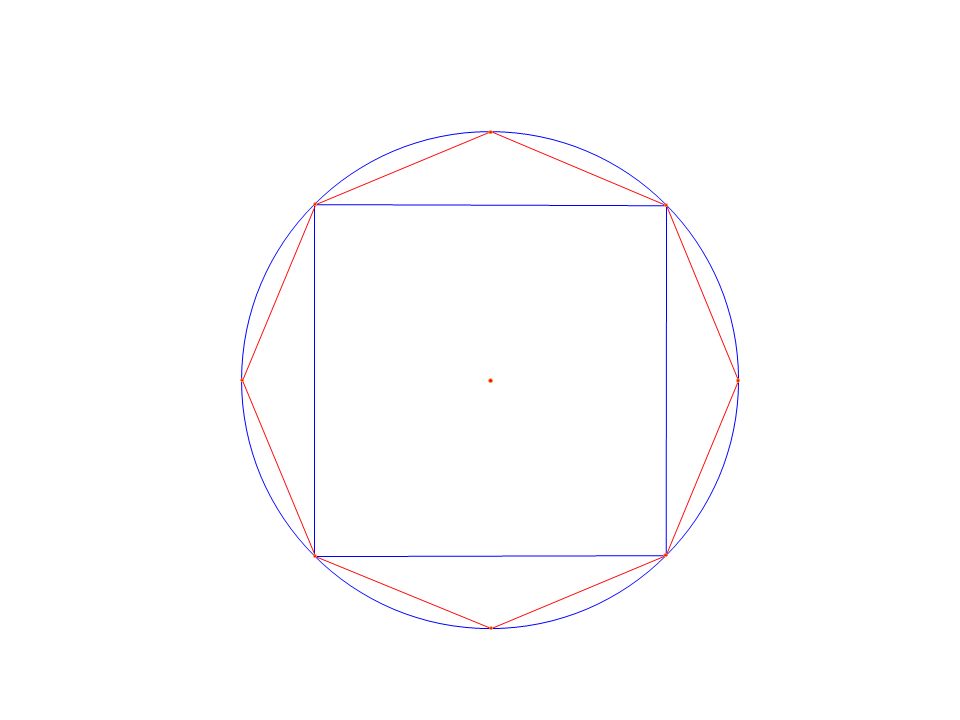
L'ottagono è quindi la connessione umana tra la terra e l'universo, l'ascensione dell'uomo dal peccato allo stato di perfezione. Questo argomento è affrontato in modo più esauriente da altri studiosi (Götze 1998, 117, Cardini 2000, 57).

L'ottagono di base è disegnato intorno al quadrato di base, che è considerato la forma geometrica iniziale. Gli studiosi riferiscono che il quadrato era la forma geometrica iniziale nell'antichità per costruire l'ottagono geometricamente (Götze 1998, 115-117 e 164-165).

Una misura logica per il quadrato di base, che è associata alla terra, sarebbe una misura terrena. Una di queste misure in senso astrologico è il numero di giorni in un anno sulla terra. Si teorizza quindi che l'ideazione del concetto per Castel del Monte possa essere iniziata da un quadrato di base le cui due diagonali sommate sono uguali in unità lineari al numero di giorni sulla terra, Fig. 8.

Fig. 8. Ispirazione per la dimensione del quadrato di base.

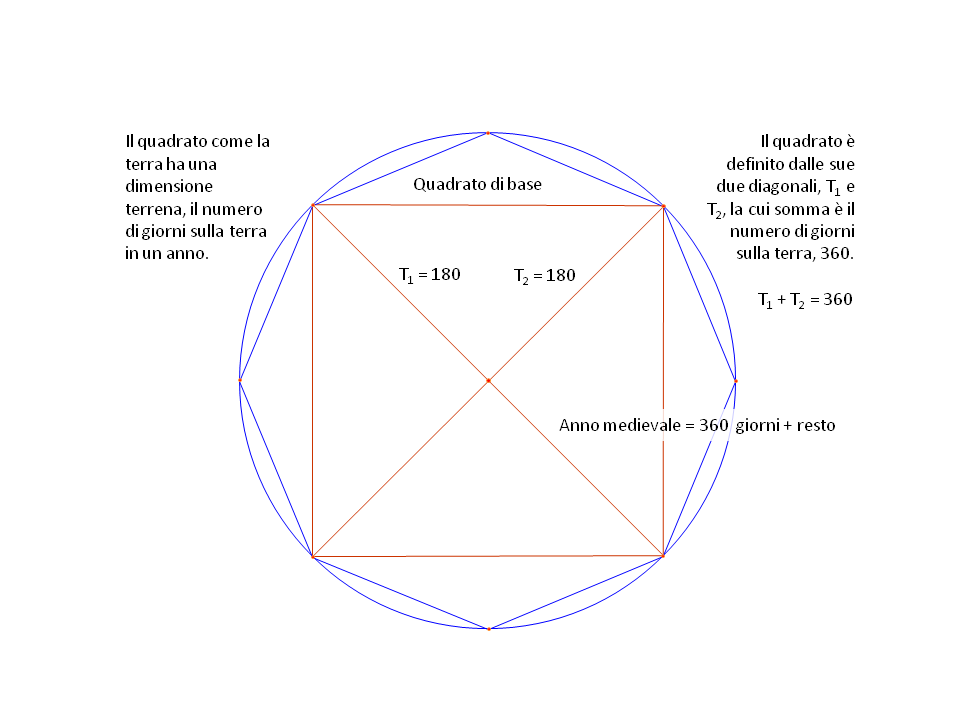
La somma di due diagonali potrebbe essere perché il quadrato ha due diagonali, oppure perché ci sono due quadrati all'interno dell'ottagono, due piani at castello, ecc., Fig. 7 e 8.

L'anno era comunemente considerato nel Medioevo di avere 360 giorni più un resto di giorni. La diagonale quindi sarebbe di 180 unità (360 giorni diviso due per due diagonali). Di conseguenza, il lato del quadrato di base è di 127,279 unità, Fig. 9.

Fig 9. Lato del quadrato di base derivato dalla relazione pitagorica.

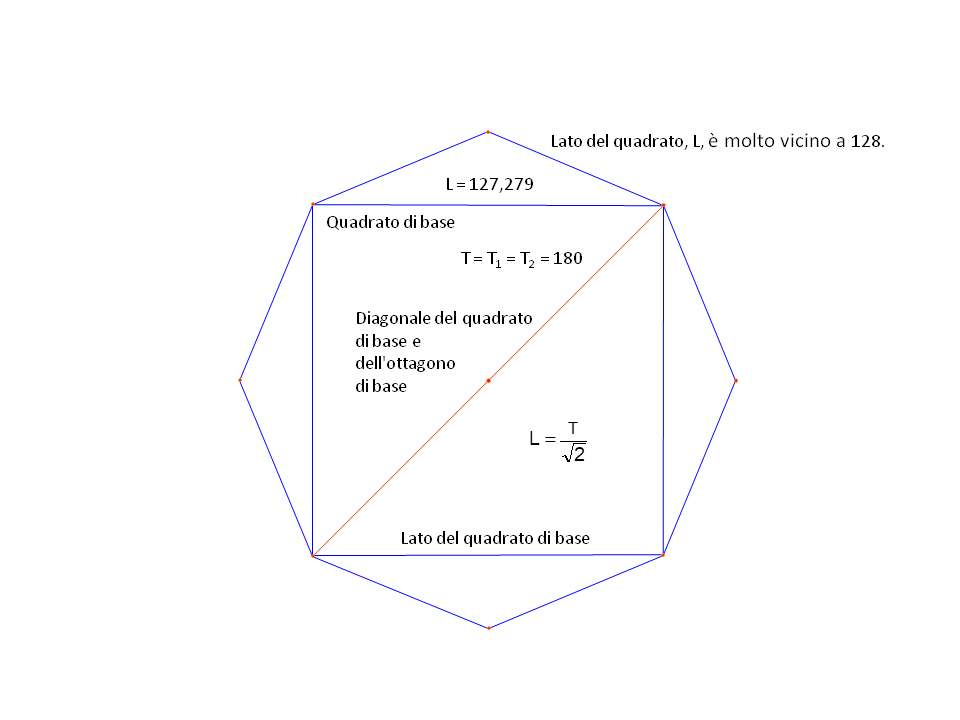
Scegliendo un lato di 128 unità per il lato del quadrato di base si ottiene una dimensione diagonale che, raddoppiata per due diagonali o due quadrati, produce 362,04 unità, Fig. 10.

Fig. 10. Teorizzata dimensione del quadrato di base, L = 180.

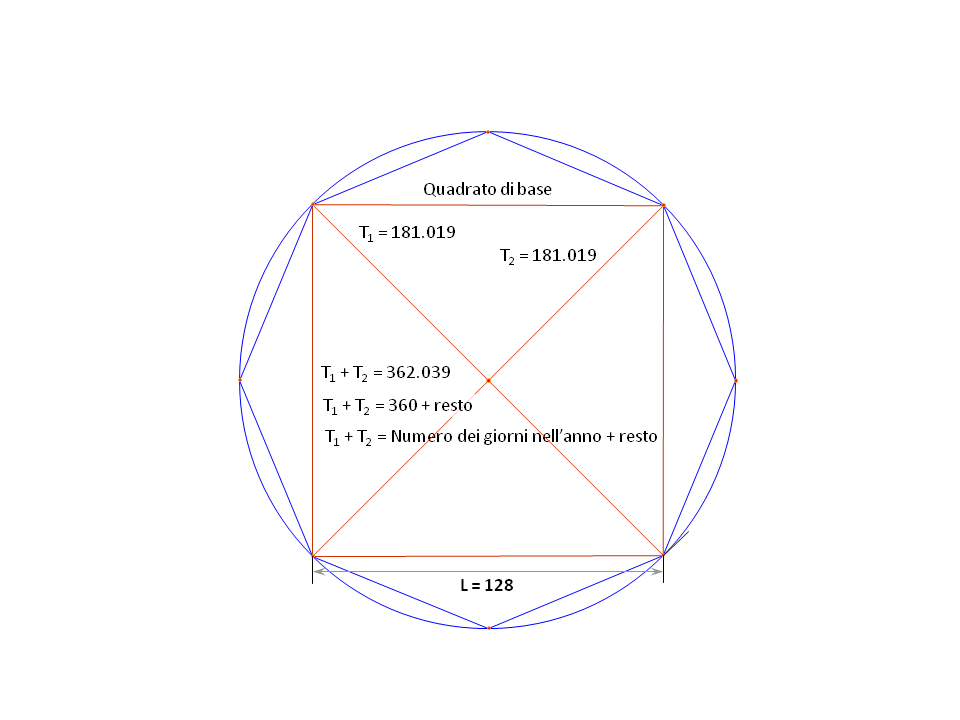
Certe relazioni e costanti matematiche erano conosciute come approssimazioni nell'antichità, molto più di oggi; le approssimazioni facilitavano l'uso comune nei calcoli di tutti i giorni. La radice quadrata di 2 (√2) era comunemente approssimata a 1,4; al giorno d'oggi questa quantità è relegata alla funzione di un tasto su una calcolatrice.

Gli antichi matematici erano consapevoli che c'era un resto, la differenza tra il valore reale di √2 (1,414136 ...) e 1,4. La percezione era che il resto era un'imperfezione che poteva essere ignorata, sebbene nella costruzione geometrica quest'approssimazione di 1,4 fosse evidente, e ignorarla porterebbe a errori.

Lo stesso vale per il numero di giorni in un anno. L'anno era approssimato a 360 giorni. Gli altri 5 giorni erano considerati imperfezioni, in realtà giorni bonus alla fine dell'anno.

Non è diverso nei tempi moderni quando l'anno viene definito di 365 giorni con un giorno bonus ogni quarto anni (l'anno bisestile), e ci dimentichiamo chiaramente delle altre "imperfezioni", i minuti e i secondi che vengono ignorati ma compongono l'esatto anno solare (l'anno solare tropicale è di 365,24219878 ... giorni).

Abbiamo in queste approssimazioni la genesi per una soluzione al dimensionamento del quadrato di base. Il numero 360, il numero di giorni in un anno, aveva un significato particolare e persino mistico. Rendendo la diagonale di base, T, uguale a 360/2 unità (180), L è 128 unità usando 1,4 per √2 e trascurando la rimanente frazione, un'imperfezione. Il valore corrispondente per l è 64 unità. Rendere T uguale a 360 avrebbe comportato un castello troppo grande; dopotutto ci sono due diagonali in un quadrato, la cui somma è 360 quando ciascuna diagonale misura 180.

La misura di 128 unità per L è propizia, perché il quadrato quartile (quello che si ottiene dopo aver diviso il quadrato di base in quattro parti uguali) ha un diametro che è il raggio del cerchio circoscritto al quadrato di base e l'ottagono di base, Fig. 11.

Fig. 11. Dimensioni del quadrato di base ed il quadrato quartile.

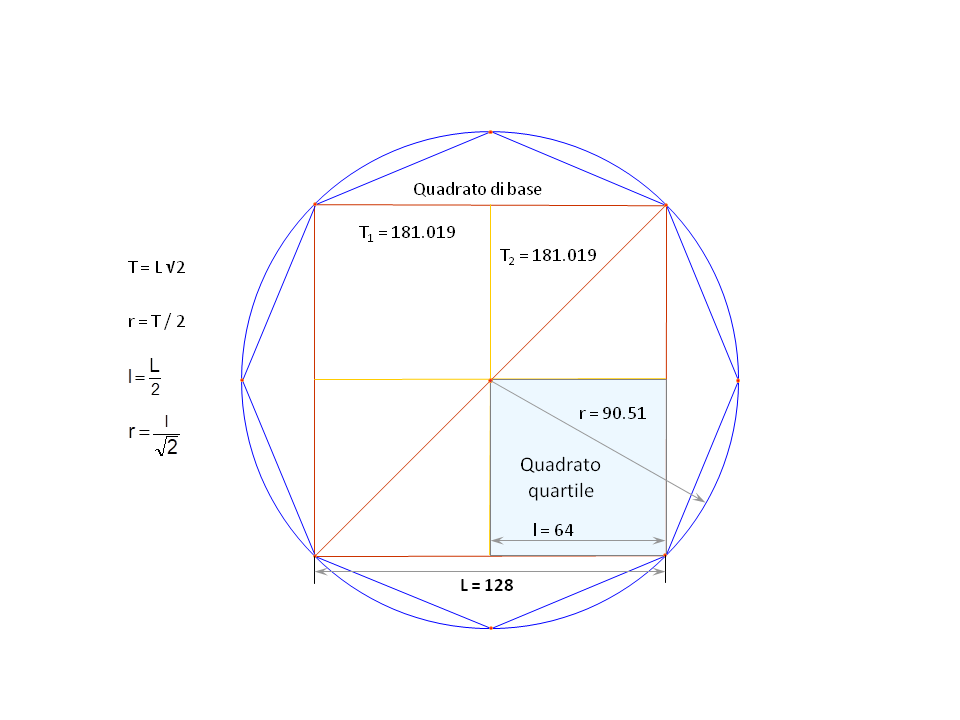
Il lato del quadrato quartile è di 64 unità (metà del lato del quadrato di base). Questo numero è il risultato del prodotto di due otto, 8 x 8 = 64. Otto è il numero mistico di questo castello. È anche opportuno notare che il castello ha otto torri, ciascuna con otto lati, e il loro prodotto è 64. Inoltre, ci sono due piani, ciascuno con otto stanze; due otto nel prodotto che produce 64.

La coincidenza di questi numeri, 360, 180, 128 e 64, e le connessioni mistiche di 360 come il numero di giorni in un anno, e 64 come il numero di lati delle torri ottagonali è ineludibile oggigiorno e deve essere stato conosciuto anche nel superstizioso Medio Evo.

Mentre questi possono sembrare argomenti per i numerologi, potrebbero essere stati benissimo nella mente dei progettatori medievali quando hanno deciso la misura del quadrato di base.

La dimensione di 128 unità è la misura adottata nel modello matematico per il quadrato di base; è la migliore ipotesi a questo punto, ma alla fine viene confermata dai risultati.

____________________

Ref.

Cardini, F. 2000. Castel del Monte. Bologna: Il Mulino.

Götze, H. ed. 1998. Castel del Monte, Geometric Marvel of the Middle Ages. New York: Prestel-Verlag.