Pagina 6
Esame dell'Unità di Misura
Avendo stabilito una dimensione per la misura primaria, un quadrato di base con un lato di 128 unità, rimane una sola incognita nel modello matematico; queasta è la dimensione dell'unità di misura utilizzata dalgl architetti e costruttori medievali a Castel del Monte.
Qualsiasi unità di misura proposta può essere testata con il modello matematico, inserendo il suo valore metrico nel spreadsheet, la cella F11 del foglio di calcolo a pagina 3, e lasciando che il spradsheet calcoli le dimensioni delle molte variabili. Il valore per l'unità di misura che fornisce la migliore corrispondenza tra le dimensioni risultanti nel spreadsheet e le attuali misure deve essere logicamente l'unità di misura utilizzata dagli architetti nella progettazione e costruzione di Castel del Monte.
Poiché ci sono dozzine di variabili e oltre cento formule nel modello matematico, stabilire una corrispondenza tra le misure teorizzate e quelle effettive richiede un'esame iterativo. L'esame è complicato da una serie di circostanze.
Non tutte le dimensioni per le variabili nel modello matematico sono conosciute o disponibili per quest'analisi. Studiosi si son fermati su diversi aspetti del castello, avanzando diverse teorie. Le dimensioni su cui essi si concentrano e per le quali riportano le dimensioni nella letteratura non sono necessariamente per le variabili in questo modello matematico.
Questo studio si basa principalmente su misure riportate lella letteratura/stampa. Le fonti più ampie e autorevoli di varie dimensioni sulla planimetria sono Götze e Shirmer, rispettivamente Fig. 12 e 13.
Fig. 12. Dimensioni della pianta – Götze
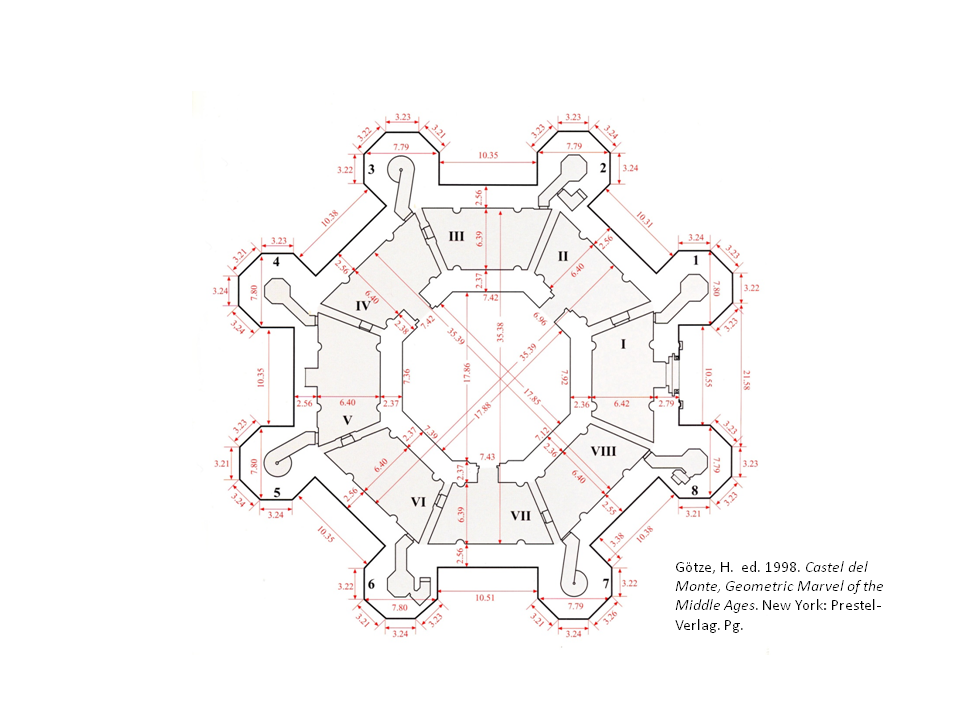
Fig. 13. Dimensioni della pianta – Shirmer.

Un'altra complicazione è che le misure includono u'incertezza dovuta a un numero di fattori. La più significativa è l'incertezza dovuta ad errori di misurazione per i valori riportati nella letteratura, che non sono del tutto evitabili.
Alcune dimensioni sono note con grande certezza perché vengono misurate con maggiore precisione e ripetutamente per le numerose istanze di questa dimensione. Uno di questi per esempio è la misura per i 32 lati uguali delle torri fornite da Götze. Le numerose istanze di questa misura forniscono un mezzo per perfezionare ulteriormente la misura nominale del lato ottagonale della torre, usando la statistica di 32 misure.
La dimensione della zoccolatura delle torri, che è considerata una caratteristica ornamentale dagli studiosi ed è fisicamente meno facile da misurare con precisione, è menzionata in modo deferenziale da Götze con un singolo valore, ed è conosciuta con meno precisione.
Vi sono ulteriori incognite che contribuiscono prevedibili deviazioni, e che influisono nel confrontare i predicati del modello matematico con le misure effettive ed intese. Alcune deviazioni derivano dalle capacità per una precisa esecusione da parte dei costruttori medievali, e dall'esattezza con cui riprodussero le dimensioni dai piani degli achitetti.
È rimarchevole il livello di precisione raggiunto dagli achitetti e costruttori medievali, sia nella progettazione che nella costruzione, visto che infine le misure predicate dal modello matematico differiscono nell'aggregato dalle attuali misure di meno di quattro parti su diecimila (0,4%), come mostrato più avanti.
Un'ultima considerazione è l'estrema gamma di dimensioni predicate dal modello matematico, che poi devono essere confrontate con le misure attuali.
La ricerca dell'unità di misura comporta il confronto di variabili con misure molto grande e variabili con misure molto piccole allo stesso tempo, e in presenza d''incertezze sulle attuali misure.
Un esempio di dimensioni estremamente diverse è la diagonale maggiore dell'ottagono di base T, che è di circa 56 m, e lo strato di finitura dei muri interni v, che è di circa 4,5 cm; uno essendo più di mille volte più grande dell'altro.
La ricerca iterativa dell'unità di misura si concentra su due dozzine di variabili chiave per le quali le misure sono note con ragionevole certezza, Fig. 12 e Fig. 13.
La Tabella 1 mostra le variabili chiave per le quali sono disponibili le misure e la loro fonte.
Tabella 1. Variabili del modello matematico con misure.
| No. | Variabile | Misura | Fonte |
|---|---|---|---|
| 1 | f | 0,380 m | Lanera |
| 2 | m | 0,154 m | Lanera |
| 3 | u' | 7,768 m | Götze |
| 4 | s' | 3,229 m | Götze |
| 5 | ss' | 3,543 m | Lanera |
| 6 | tt' | 9,283 m | Schirmer |
| 7 | a' | 2,560 m | Götze |
| 8 | c26" | 28,450 m | Shirmer |
| 9 | h26" | 26,290 m | Shirmer |
| 10 | c18" | 23,810 m | Shirmer |
| 11 | h14" | 20,258 m | Shirmer |
| 12 | h12" | 17,696 m | Shirmer |
| 13 | wg | 6,401 m | Shirmer |
| 14 | h6g" | 11,287 m | Shirmer |
| 15 | h2g" | 8,930 m | Götze |
| 16 | bg" | 2,370 m | Götze |
| 17 | ddt18" | 10,396 m | Shirmer |
| 18 | ddf18" | 9,625 m | Shirmer |
| 19 | pg" | 1,050 m | Shirmer |
| 20 | d2" | 7,380 m | Shirmer |
La ricerca consiste nell'assegnare un valore metrico all'unità di misura (cella F11), lasciando che il spreadsheet dia i risultanti valori predicativi, e misurando in ogni caso la deviazione nell'aggregato fra i valori predicati e le attuali misure come riportate nella Tabella 1 per le selezionate variabili.
La deviazione complessiva è calcolata come la somma delle deviazioni delle singole variabili (il valore della deviazione assoluta, ignorando il segno della deviazione). La dimensione che fornisce la deviazione più bassa è considerata quella che fornisce la migliore corrispondenza è quella che è da considerasi la corretta unità di misura nella progettazione di Castel del Monte.
____________________
Ref.
Götze, H. ed. 1998. Castel del Monte, Geometric Marvel of the Middle Ages. New York: Prestel-Verlag.
Shirmer, W. ed. 2000. Castel del Monte. Research results of the years 1990 to 1996. Mainz. ISBN 3-8053-2657-2

