Pagina 7
Determinazione dell'Unità di Misura
Il risultato dell'analisi iterativa con il spreadsheet (foglio di calcolo) per l'unità di misura è mostrato graficamente nella Fig. 14.
Fig. 14. Ottimizzazione dell'unità di misura di Castel del Monte.
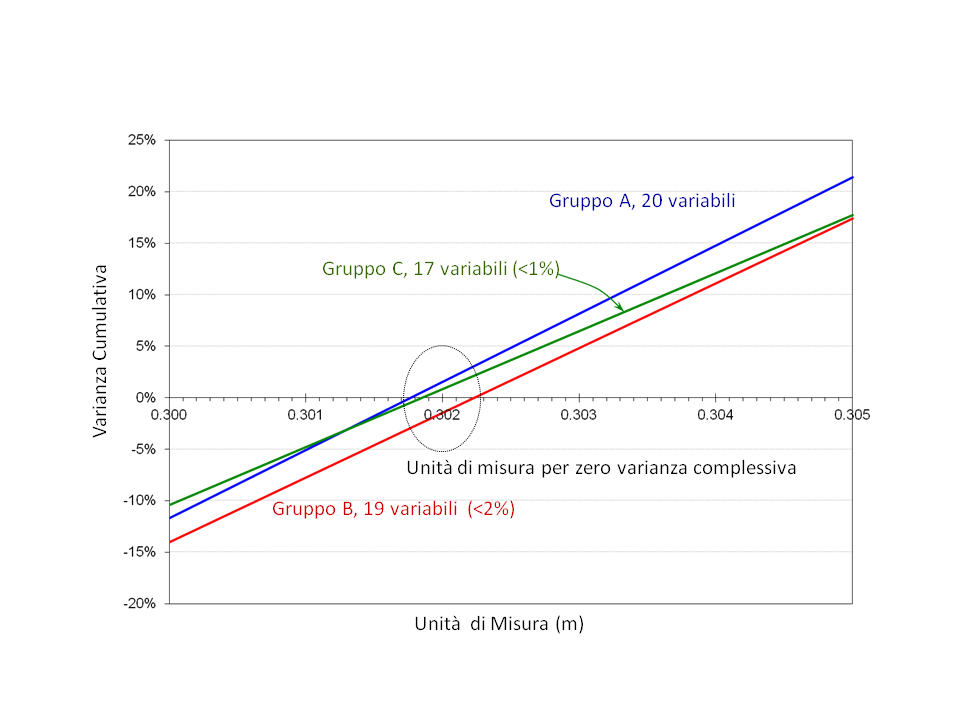
La varianza complessiva è analizzata anche per due altri gruppi di variabili, leggermente diversi dal gruppo di 20 variabili designato inizialmente (Tabella 1, pg. 6). Il motivo è la gamma di queste varianze e le circostanze associate alle variabili con le maggiori deviazioni.
La varianza delle individuali variabili è mostrata graficamente in Fig. 15, per l'unità di misura di 0,3020 m.
Fig. 15. Varianze per l'unità di misura di 0,3020 metri
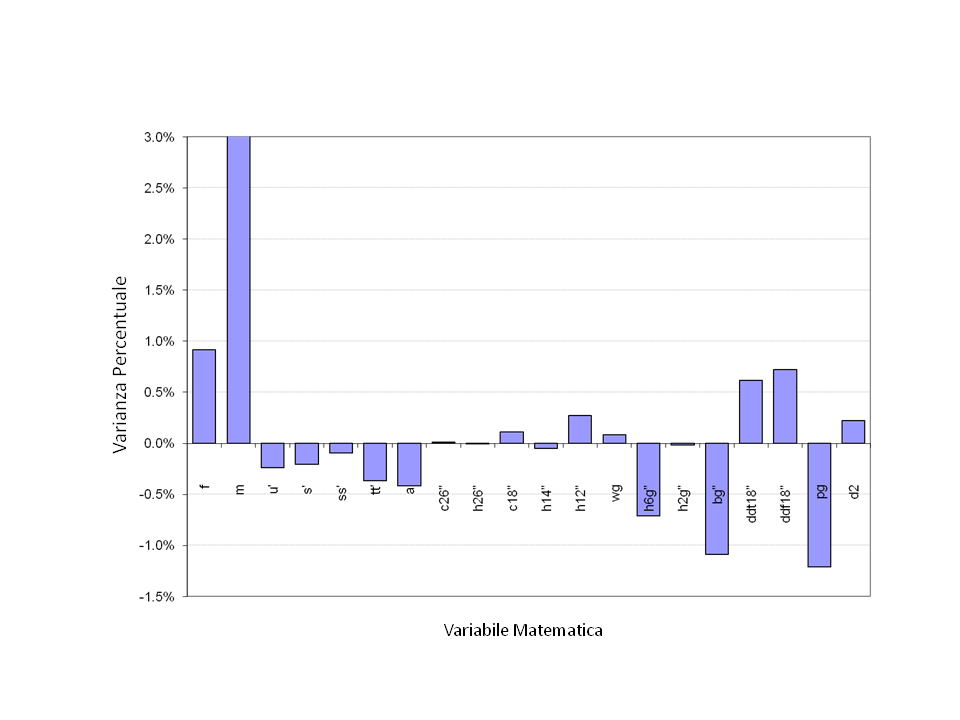
La deviazione complessiva è considerata per:
- tulle le 20 variabili -- Gruppo A in Fig. 14
- 19 variabili, escludendo varianze superiori al 2%, -- Gruppo B in Fig. 14
- 17 variabili, escludendo varianze superior al 1% -- Gruppo C in Fig. 14
Le varianze sono riportate nella Tabella 2.
Tabella 2. Analisi delle varianze per l'unità di misura di 0,302 m.
| No. | Variabile |
Predicata
(metri) |
Misurata
(metri) |
Varianza
(metri) |
Varianza
(%) |
Gruppo-A
Assoluta |
Gruppo-B
Assoluta |
Gruppo-C
Assoluta |
|---|---|---|---|---|---|---|---|---|
| 1 | f | 0,383 | 0,38 | 0,004 | 0,92% | 0,92% | 0,92% | 0,92% |
| 2 | m | 0,159 | 0,154 | 0,005 | 3,25% | 3,25% | ||
| 3 | u' | 7,776 | 7,80 | -0,022 | -0.28% | 0,28% | 0,28% | 0,28% |
| 4 | s' | 3,221 | 3,23 | -0,008 | -0,25% | 0,25% | 0,25% | 0,25% |
| 5 | ss' | 3,539 | 3,54 | -0,004 | -0,11% | 0,11% | 0,11% | 0,11% |
| 6 | tt' | 9,247 | 9,28 | -0,036 | -0,39% | 0,39% | 0,39% | 0,39% |
| 7 | a' | 2,549 | 2,56 | -0,011 | -0,43% | 0,43% | 0,43% | 0,43% |
| 8 | c26" | 28,453 | 28,45 | 0,000 | 0,00% | 0,00% | 0,00% | 0,00% |
| 9 | h26" | 26,287 | 26,29 | -0,003 | -0,01% | 0,01% | 0,01% | 0,01% |
| 10 | c18" | 23,830 | 23,81 | 0,025 | 0,11% | 0,11% | 0,11% | 0,11% |
| 11 | h14" | 20,247 | 20,26 | -0,011 | -0,05% | 0,05% | 0,05% | 0,05% |
| 12 | h12" | 17,745 | 17,70 | 0,049 | 0,28% | 0,28% | 0,28% | 0,28% |
| 13 | wg | 6,411 | 6,40 | 0,010 | 0,16% | 0,16% | 0,16% | 0,16% |
| 14 | h6g" | 11,202 | 11,29 | -0,085 | -0,75% | 0,5% | 0,5% | 0,5% |
| 15 | h2g" | 8,928 | 8,93 | -0,002 | -0,02% | 0,02% | 0,02% | 0,02% |
| 16 | bg" | 2,340 | 2,37 | -0.030 | -1,27% | 1,27% | 1,27% | |
| 17 | ddt18" | 10,462 | 10,40 | 0,066 | 0,63% | 0,63% | 0,63% | 0,63% |
| 18 | ddf18" | 9,696 | 9,63 | 0,071 | 0,74% | 0,74% | 0,74% | 0,74% |
| 19 | pg" | 1,038 | 1,05 | -0,012 | -1,14% | 1,14% | 1,14% | |
| 20 | d2" | 7,396 | 7,38 | 0,016 | 0,22% | 0,22% | 0,22% | 0,22% |
| N | 20 | 19 | 17 | |||||
| Media | 0,55% | 0,41% | 0,31% |
Il gruppo B esclude la variabile m perché ha una dimenione minuscola
che aggrava la varianza. La dimensione di m è di 15,4 cm;
la varianza dalla misura predicata è di soli cinque millimetri, tuttavia la varianza in percentuale è di 3,25%.
Il gruppo C esclude altre due variabili, bg" e pg, con varianze tra 1% e 2%, a causa di alcune circostanze uniche. La varianza per bg" è di 3 cm per una dimensione di 2,37 m; è una carenza minuscola ma significativa in percentuale, associata alla strato di finitura delle pareti interne. La variabile pg è la larghezza del muro di separazione; la varianza è di soli 12 mm. Questa variabile non fa parte dell'algoritmo geometrico, è stata definita euristicamente.
Un'ispezione di Fig. 14 indica che l'unità di misura è nell'intervallo fra 0,3018 m e 0,3022 m, con un ravvicinamento verso la misura di 0,3018 m. Questo è un intervallo di mezzo millimetro. L'unità di misura è quindi approssimata a 0,3020 m, con una precisione di ± 1 mm.
Questa unità di misura fornisce una varianza media dello 0,31% per 17 variabili chiavi (Tabella 2).
I dati indicano anche che questo modello matematico, con un'unità di misura di 0,302 m, predice le misure complessive della planimetria con una varianza minore del 0,55% e una certezza statistica del 95%.
Questo è un risultato di precisione significativo, da cui si inferisce la corretezza dell'algoritmo di progettazione geometrica. La predizione di tutte le forme geometriche in tutti i dettagli della planimetria, e la predizione delle loro dimensioni con una deviazione complessiva inferiore allo 0,55% è la prova che gli algoritmi geometrici risultati da questa ricerca sono corretti.
Questo è il processo di progettazione seguito dagli architetti e costruttori medievali. Non è un risultato casuale, a causa della complessità degli algoritmi e dell'elevato numero di variabili involte.
Questa è anche una testimonianza del grande talento degli architetti e costruttori medievali. Vale la pena ripetere che è perché gli architetti medievali hanno seguito un rigoroso algoritmo e i costruttori hanno realizzato la costruzione con estrema precisione che abbiamo avuto l'opportunità di decifrare il diseno oggi riportato in pietra.
I risultati sull'unità di misura danno anche prova alla dimensione data inizialmente alla misura del lato del quadrato di base, L = 180 unità; una misura per primo razionalizzata da motivi religiosi e mistici del medioevo, pg. 5.
Un quadrato di base con una dimensione laterale di 128 piedi e una misura di 0.302 metri per il piede di Castel del Monte forniscono la migliore corrispondenza tra le dimensioni nella planimetria come previsti dagli algoritmi geometrici e le misure come riportate da Götze e Shirmer.
È auspicabile avere una prova fisica al castello per questa unità di misura. La ricerca è resa più facile avendo l'ascritta misura per la dimensione del "piede" di Castel del Monte.
Uno di questi candidati è il concio di coronamento dello zoccolo (f), Fig. 16.
Fig. 16.Concio di coronamento della zoccolatura alla base delle torri.
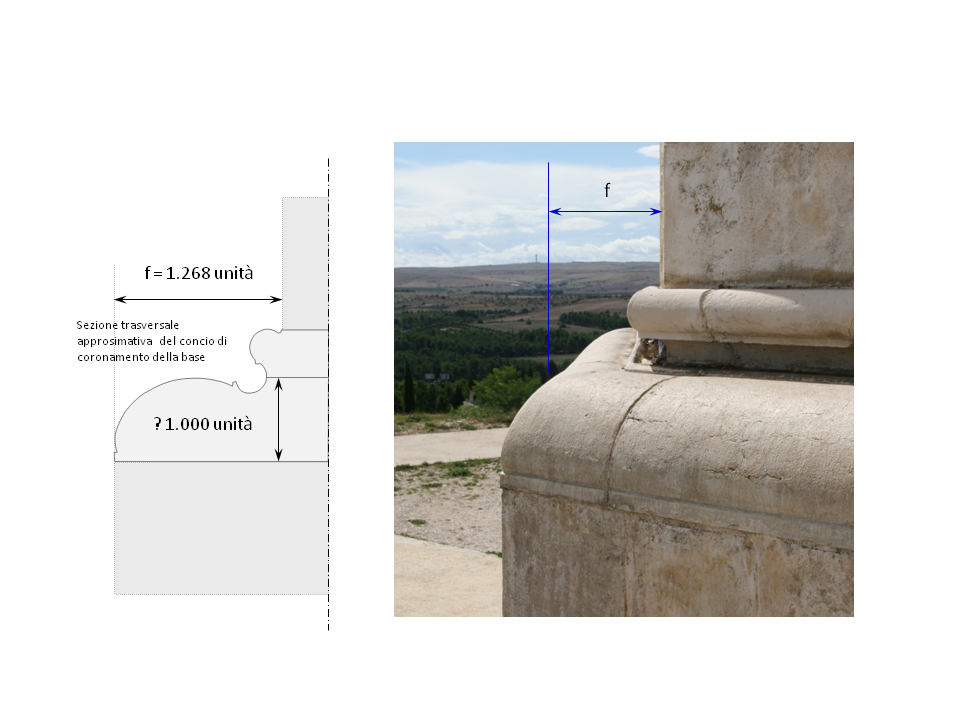
La sezione trasversale dei conci che ricoprono la zoccolatura alla base delle torri ha un sagoma decorativa complessa all'esterno e un angolo quadrato sul lato opposto, incastonato nella muratura della torre. La sezione trasversale ha una larghezza lineare leggermente più grande della largezza dello zoccolo f per consentire che una porzione di questo concio venga incorporata nella muratura della torre.
Si ipotizza che l'altezza di questi conci potrebbe essere l'unità di misura di Castel del Monte. Non avendo altre basi razionali o geometriche per fissare l'altezza di questo elemento, si è pensato che gli architetti potrebbero aver scelto un'altezza esattamente ugulale al "piede di Castel del Monte" per questo concio, 0,302 m. Come l'altra misura di questo concio, f, è "fondamentale" nel disegno geometrico della planimetria, così è "fondamentale" la misura del piede nella costruzione del castello.

