What is a Gradient? |
|
|
|
Simply put, a gradient indicates
how a physical quantity varies over a specified direction.
This physical quantity can be anything.
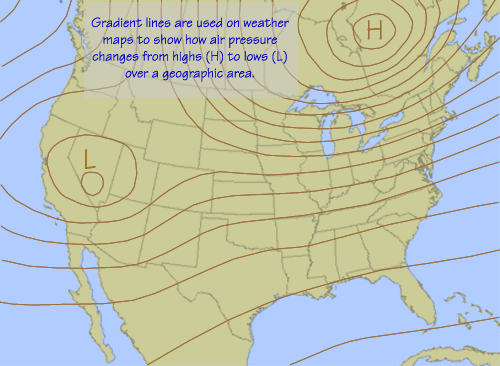
A familiar example of gradients is the lines on weather maps that indicate
air pressure gradients as
isobars. |
 |
 
|
 Stairs are Gradients
Stairs are Gradients |
|
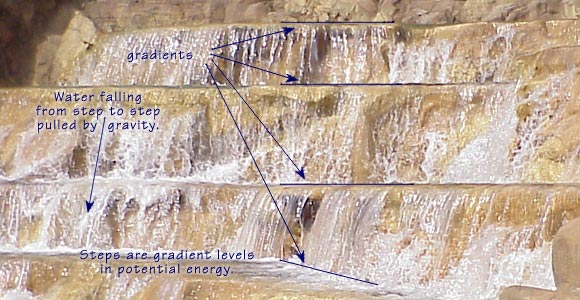
A flight of steps is a physical example of a gradient
dealing with elevation. A step is the line along which the elevation remains
the same. Adjacent steps represent one elevation level up or down from the
current one. |
 |
 
|
|
Current flowing through the earth can be visualized as water flowing down these steps.
As gravity pulls the water down one step, water loses potential energy (the ability to
do work, as in hydroelectric plants). The energy level between the higher steps
and the lower steps drives the water. Similarly, voltage gradients are
associated with current flowing through the earth across gradient lines. |
 |
 
|
 Simple Gradients
Simple Gradients |
|
Gradients in real situations are complex and variable;
a weather map is a good example of how detailed and changeable they can be.
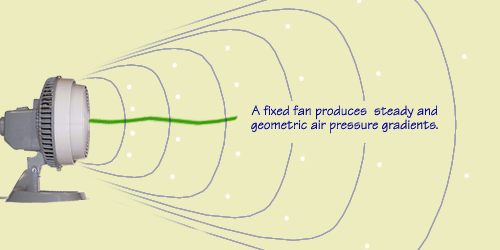
There are simpler and more stable situations, however.
For example, a fan fixed in one place creates airflow with a
steady and geometric gradient pattern. |



|
|
Gradients associated with power systems have unique patterns.
Although in real life these gradients can be very complicated, there are features
that recur often and dominate the entire pattern. We will explore some of these
dominant features in a simple study case. |
 
|
 Voltage Gradient Study Case
Voltage Gradient Study Case |
|
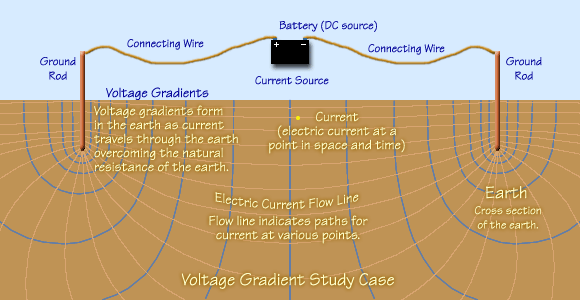
The simplest case for studying voltage gradients in the earth is that of two electrodes
installed in the earth's surface with a voltage applied between them to drive current
through the earth. The electrodes are
installed
at a great distance from each other, in an open field, with no pipelines or
any other metallic structures buried in or connected to the earth. |



|
 
|
|
The gradient pattern is the same whether it is direct current, like a car battery, or alternating current,
like an alternating current generator or a commercial electric power source.
|
|
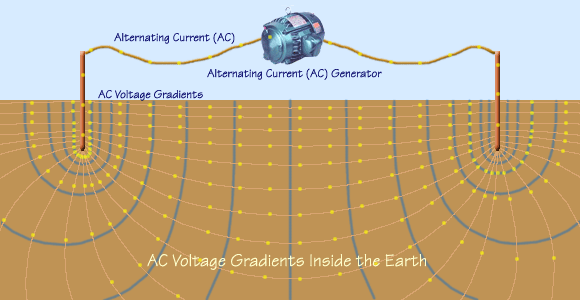
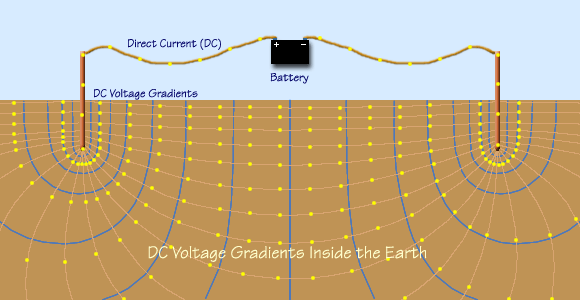
The following is a visualization of the current flowing through the earth between the
two electrodes and creating voltage gradients. The figure shows the voltage gradients
when an alternating current source is connected between the two rods. Current spreads
out through the earth, following characteristic lines that follow physical laws. Voltage
gradients form in the earth and on its surface as the current overcomes the earth's
resistance. These gradients are shown in the figure as lines along which the voltage
potential is the same. The separation between lines indicates how quickly gradients
rise to the next voltage level. In other words, the steepness of the gradients (how
close together the lines are) indicates how rapidly the voltage is changing. The
gradients themselves alternate as a result of alternating currents.
|



|
 
|
|
The distribution of these voltage gradients is related to current flow. The gradients
form characteristic patterns rooted in physical laws. These patterns have almost nothing
to do with the alternating nature of the current, but much to do with the shape of the
electrodes, their distance from each other, and soil characteristics. Notice the
symmetry of these complex patterns between the left and right electrodes. Nearly the
same voltage gradient pattern results if we use a direct voltage source causing direct
current to flow through the earth between the same electrodes, as shown in the next
figure. |



|
 
|
|
The spatial features of the voltage gradients—how they are spaced and curved—are nearly
the same whether the current is AC or DC. The voltage gradient itself will be AC or DC
depending on the type of current causing the gradient, but the physical shape and
distribution of the voltage gradients in the earth between the two electrodes will be
the same in either case. |
|
We will use the direct current representation of voltage gradients for the remainder of
this presentation. Doing so allows us to avoid the technical complexities of an
alternating current discussion while retaining focus on the issue of voltage gradients
as the source of stray voltage.
|
 
|
|
The pattern of the gradients—the way they distribute themselves between the two
electrodes—is independent of the current level. This is evident in the AC animation above
(click on "show me" for the AC voltage gradients figure above). The gradient's intensity
(steepness) varies with the intensity of the current, but the gradient's distribution and
shape remain fixed. Again, this is because the gradient's shape and distribution are
determined by the electrode's size, shape, and location, and the soil's characteristics.
The amount of current determines only the voltage gradient's strength. This
differentiation will become particularly significant as we investigate the sources of
actual gradients on power systems. |
|
The core portions of the voltage gradients form inside the earth where they are out of
reach of animals and people. However, these gradients do extend to the surface of the
earth where different voltage levels can be simultaneously touched by animals. The
next figure shows these voltage gradients as they appear on the surface of the earth
from an elevated viewpoint. |
 
|




|
 
|
|
The voltage gradients vary from point to point between the two electrodes, but are not
evenly distributed. They are very steep near the electrodes, and spread-out in the middle
between them. The current that enters the earth creating the voltage gradient is of a
predetermined quantity. Near the points where the current enters or leaves the earth,
the current has a high density because it is concentrated in a small area. In the large
area between the two electrodes, the current becomes very diffuse. The low current
density results in small voltage gradients. For the sake of a simple presentation,
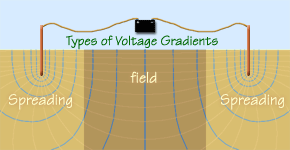
gradients will be classified as one of two types. |
|
 
|
|
The first type includes the current funneling area around the electrodes. As the
current is channeled in or out of the electrodes, the area through which the
current passes becomes smaller near the electrode, the current density increases,
and the resulting voltage gradients become steeper. The spreading effect
dominates this area; we will call these gradients
spreading gradients [Spreading Gd].
The second category is the gradient type in the open field far away from the
electrodes. At this location, because the earth conductor is large, current density
and the resulting changes in voltage gradients are small. There is no more spreading
and the gradients are regular and uniform; we will call these
field gradients [Field Gd]. |
|
|





|
